Daehyunii's Dev-blog
[데브코스] TIL-104 스택 본문
오늘 강의는 자료구조와 알고리즘 관련 강의였다. 그 중에서도 스택과 연결 리스트를 중점적으로 공부했다. 기존에 그래도 한 번 공부했던 내용이여서 그런지 내용적인 측면에서는 큰 어려움은 없었다. 다만 연결 리스트를 구현하기 위해서 클래스를 생성하고 코드를 구현하는 것이 조금은 낯설게 느껴지긴 했다. 그리고 또 스택을 활용하는 방법에 대해서도 조금 더 다양하게 활용할 수 있는데 단순히 push(), pop() 만을 활용하려는 틀에 박힌 사고를 하고 있다는 반성도 하게 되었다. 앞서 스택과 관련해서 내용을 정리한 부분들이 있지만, 다시 한 번 정리해 보려 한다.
스택이란?
stack?
데이터를 일시적으로 저장하기 위해 사용하는 자료구조이다. 데이터의 입력과 출력 순서는 후입선출(LIFO : Last In First Out)이다. 어떤 특정 자료구조를 의미하는것이 아닌 추상적인 의미로 데이터를 후입선출 구조로 활용해서 코드를 구현하면 그것이 바로 스택이다. 현실에서 설거지 그릇을 생각하면 좋다. (설거지를 할 때 가장 나중에 쌓아 놓은 그릇을 설거지를 할 때는 가장 먼저 집어들어 설거지를 하게 되므로)
앞서 말했듯이 스택은 추상적인 의미로, 구현할 수 있는 방법은 굉장히 많다. JavaScript에서는 배열을 통해 구현하는것이 일반적이다.
- push( ), pop( ) 메서드를 활용하는 방법
- unshift( ), shift( ) 메서드를 활용하는 방법 (배열의 특성한 index를 갖기 때문에 배열의 가장 앞에서 상태를 변화시키는 unshift( )와 shift( ) 메서드는 지양하는 것이 좋다.
위의 스택을 가지고 실제로 문제를 풀어보는 실습을 했다. 스택 문제 중에서는 가장 대표적인 문제로 바로 올바른 괄호 문제이다. 이전에도 한 번 풀어본 문제여서 풀이 자체가 어렵지는 않았지만, 스택이라는 개념을 활용해서 다양한 방법으로 문제를 해결할 수도 있다는 것을 느꼈다.
문제 설명
괄호가 바르게 짝지어졌다는 것은 '(' 문자로 열렸으면 반드시 짝지어서 ')' 문자로 닫혀야 한다는 뜻입니다.
예를 들어"()()" 또는 "(())()" 는 올바른 괄호입니다.")()(" 또는 "(()(" 는 올바르지 않은 괄호입니다.
'(' 또는 ')' 로만 이루어진 문자열 s가 주어졌을 때, 문자열 s가 올바른 괄호이면 true를 return 하고, 올바르지 않은 괄호이면 false를 return 하는 solution 함수를 완성해 주세요.
제한사항
문자열 s의 길이 : 100,000 이하의 자연수문자열 s는 '(' 또는 ')' 로만 이루어져 있습니다.
<출처 - 프로그래머스 Lv2 올바른 괄호 문제>
//내가 작성한 정답
function solution(s){
let stack = [];
for(let x of s){
if(x === '('){
stack.push(x);
}else{
if(stack.length === 0){
return false;
}
stack.pop()
}
}
return stack.length === 0 ? true : false;
// return stack.length === 0;
}아마 내가 작성한 답이 일반적으로 사람들이 문제를 해결하는 방식일 것이다. 그런데 스택을 활용해서 문제를 해결하는 방법에는 꼭 배열을 만들어서 문제를 해결하는것만이 정답이 아니었다. 배열 대신 카운트 변수를 만들어 스택처럼 활용해 문제를 해결할 수도 있었다.
function solution(s){
let count = 0;
for(let x of s){
if(x === '('){
count++;
}else{
if(count === 0){
return false;
}
count--;
}
}
return count === 0;
}사실 본 문제만 놓고 봤을때는 효율성 측면에서 많은 차이가 나지는 않겠지만, 그래도 공간 복잡도 측면에서 보았을때 카운트를 세서 문제를 해결하는 것이 더 나은 방법임은 확실하다. 그리고 또 하나의 사고에 박혀 문제를 해결하는것에만 집중했었는데, 다른 알고리즘 및 자료구조를 공부할 때는 보다 넓은 시야로 문제를 해결하려고 노력해 보아야 겠다.
그리고 두 번째로 공부한 내용이 연결 리스트이다. 일반적으로는 배열을 통해서 알고리즘 문제를 해결하는 경우가 대부분 이지만 배열은 index 번호를 갖기 때문에 발생할 수 밖에 없는 문제점들을 보완하기 위해 등장한 연결 리스트에 대해서 공부를 했다.
연결 리스트란?
(단일 연결 리스트, 이중 연결 리스트, 원형 연결 리스트)
연결 리스트란, 각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 선형 자료 구조이다. 앞서 말했듯이 배열은 index 번호가 있어 필연적으로 발생할 수 밖에 없는 문제들을 연결 리스트에서는 해결이 가능하다.
- 단일 연결 리스트 : 각 노드에 자료 공간과 한 개의 포인터 공간이 있고, 각 노드의 포인터는 다음 노드를 가리킨다.

- 이중 연결 리스트 : 단일 연결 리스트와 비슷하지만, 포인터 공간이 두 개가 있고 각각의 포인터는 앞의 노드와 뒤의 노드를 가리킨다.
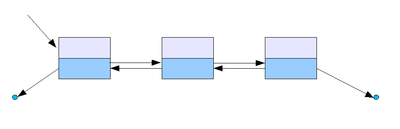
- 원형 연결 리스트 : 일반적인 연결 리스트에 마지막 노드와 처음 노드를 연결시켜 원형으로 만든 구조이다.
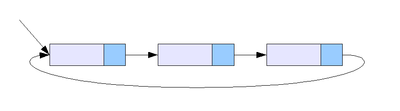
즉, 세 가지 유형은 연결하는 방식에 차이만 존재할 뿐이다. 그렇다면 배열과의 차이점은 무엇일까?
- 배열은 Index 번호를 가지기 때문에 탐색을 하는데 굉장히 빠른 자료 구조이다. 하지만 연결 리스트는 인덱스 번호가 없기 때문에 첫 노드(head라 부름)를 타고 전체를 탐색해서 원하는 노드를 찾아야 한다.
- 배열은 Index 번호를 가지기 때문에 배열의 중간에 요소를 추가하거나 제거하는 경우에는 모든 인덱스 번호가 옮겨져야 하지만, 연결 리스트의 경우에는 index번호가 따로 존재하기 않기 때문에 데이터를 중간에 추가하거나 제거하는데 빠르다. (단, 배열의 경우에도 마지막 위치에 요소를 추가하거나 삭제하는 경우에는 Index를 옮길 필요가 없기 때문에 빠르다.)
위와 같은 내용을 공부하고 강의에서 선택 과제를 내주었다. 바로 강사님이 작성해 주신 단일 연결 리스트 코드에서 '엣지 케이스'들을 찾아 작성을 해보는 것이다. 그리고 size 메서드도 추가해 보라는 주문이었다. 그래서 최대한 혼자 생각하고 해결하는 방법으로 문제를 해결해야겠다는 생각이 들어 검색이나 자료를 참고하기 보다는 스스로 생각하는데 많은 시간을 보냈다.
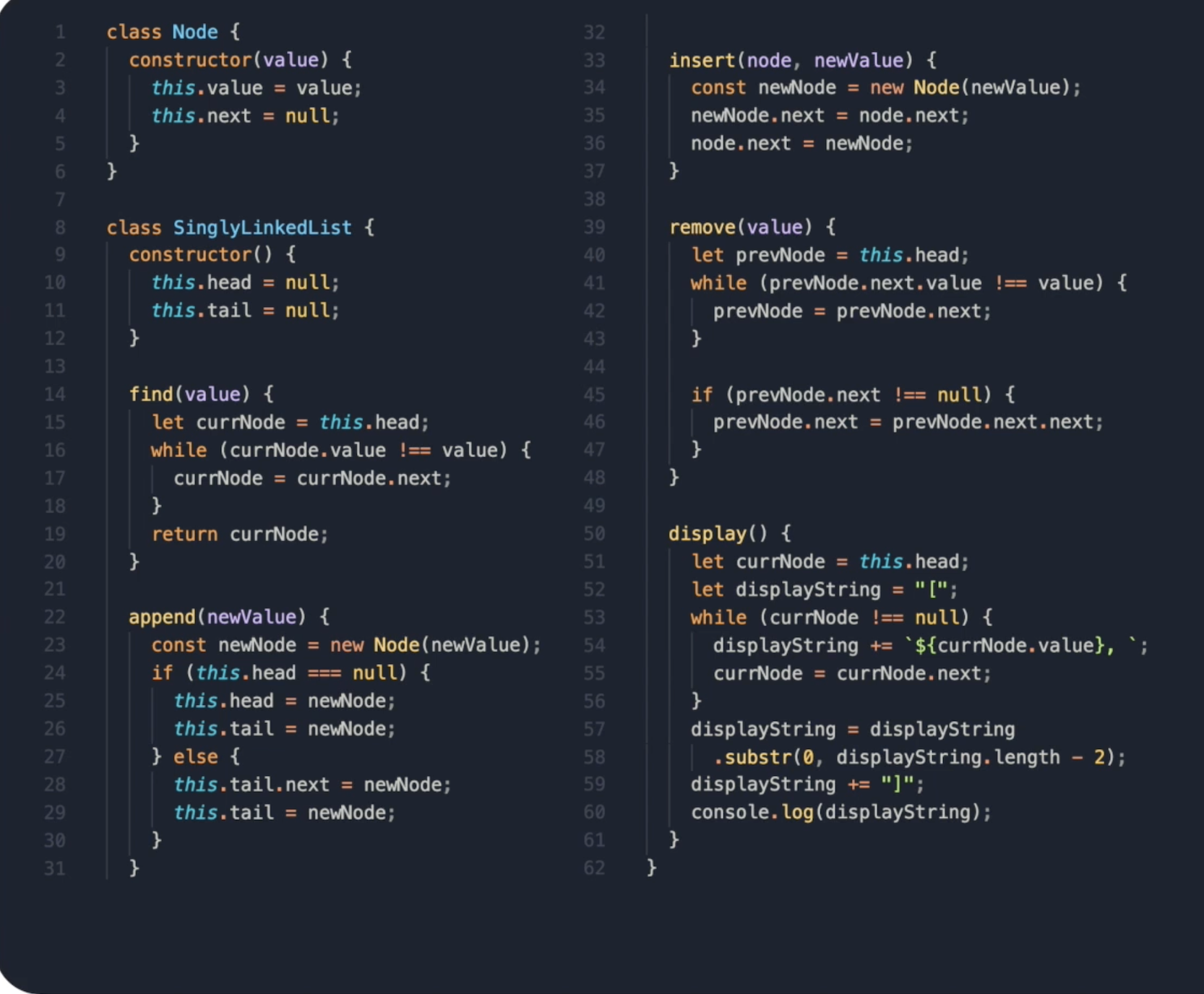
내가 찾은 엣지 케이스들이다.
class SinglyLinkedList {
constructor(){
this.head = null;
this.tail = null;
this.length = 0;
}
find(value){ // 찾고자 하는 값이 여러개인 경우 해결 방법이 없다.
let currentNode = this.head;
while(currentNode.value !== value){
if(currentNode.next !== null){ // next 프로퍼티 값이 null이 아니라면
currentNode = currentNode.next; // 그 다음 노드로 이동
}else if(currentNode.next === null){
return undefined; // 다 돌았는데 없다면, undefined 반환
}
}
return currentNode;
}
append(newValue){
let newNode = new Node(newValue);
if(this.head === null){
this.head = newNode;
this.tail = newNode;
}else{
this.tail.next = newNode;
this.tail = newNode;
}
}
insert(node, newValue){ // 헤드에 데이터를 추가하는 경우가 없다
let newNode = new Node(newValue);
let preNode = this.find(node); // 참조에 의한 전달
newNode.next = preNode.next;
preNode.next = newNode;
}
remove(value){
if(this.find(value) === undefined) return undefined; //해당 값이 애초에 연결 리스트에 없는 경우!
let prevNode = this.head;
if(prevNode.value === value){ // 삭제하고자 하는 값이 바로 헤드의 값과 일치하는 경우
if(prevNode.next === null){
this.head = null;
this.tail = null;
}else{
this.head = prevNode.next;
}
}
while(prevNode.next.value !== value){ // 삭제하고자 하는 value 이전의 node를 찾게됨
prevNode = prevNode.next;
}
if(prevNode.next.next !== null){ // prevNode의 다다음 노드가 존재하면
prevNode.next = prevNode.next.next; // 바로 그 노드로 연결
}else if(prevNode.next.next === null){ // prevNode의 다다음 노드가 존재하지 않는다면
prevNode.next = null; // 연결을 차단
this.tail = prevNode;
}
}
size(){
let currentNode = this.head;
let count = 0;
while(currentNode !== null){
currentNode = currentNode.next;
count++;
}
return count;
}
}코드가 더럽더라도,,,,,,이해해주기 바란다. 코드를 예쁘게 쓰는게 목적이라기 보다는 연결 리스트의 동작 원리를 생각하면서 해결해야 하는 엣지 케이스들은 무엇이 있는지에 초점을 맞춰 최대한 코드를 작성하고자 노력했다. 물론 강의를 듣고 선택 과제로 문제를 혼자 해결한 것이기 때문에 위 코드가 정답인지는 알 수 없으나 해당 클래스들이 정상적으로 작동하는것 까지는 확인을 했다 ㅎㅎ
오늘을 마무리 하며
오늘은 나름대로 강의에 더 집중을 해서 개인 공부시간을 많이 갖지는 못했다. 하지만 연결 리스트를 직접 작성해보고 구현해 보면서 '생각 하면 할 수 있겠는데?'라는 생각이 많이 들었다. 내가 작성한 코드가 정답이 아닐수는 있어도 적어도 연결 리스트를 구현할 때 무엇을 고려해야 하는지 어떻게 동작을 하게 되는지는 확실하게 인지한 것 같다. 아직도 다시 복습하고 익혀야 하는 자료구조들이 넘쳐나지만 이렇게 차근 차근 하나 하나 생각하며 나아간다면 분명 머리속에 저절로 그려지는 날이 올거라 믿는다.
'✏️ 2022. TIL > October (데브코스)' 카테고리의 다른 글
| [데브코스] TIL-106 (0) | 2022.10.25 |
|---|---|
| [데브코스] TIL-105 이진 탐색 트리, 이진 힙 (0) | 2022.10.21 |
| [데브코스] TIL-103 HTTP, HTTPS, 함수형 프로그래밍 (1) | 2022.10.19 |
| [데브코스] TIL-102 가비지 컬렉터, 옵셔널 체이닝, null 병합 (1) | 2022.10.18 |
| [Git / Github] TIL-101 (0) | 2022.10.08 |




